Digital & Embedded Systems

Tutorial 6 - DC Motor Control

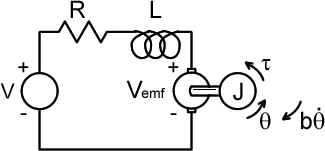
This tutorial is designed to teach you the basics of controlling the velocity of a DC motor. An electro-mechanical model of a DC motor is shown below

Electro-mechanical mode of a DC motor

V = input voltage (V)
R = nominal resistance (W)
L = nominal inductance (H)
J = Inertial load (kg*m^2/s^2)
Vemf = back emf voltage (V)
b = damping constant (Nms)
t = motor output torque (Nm)
q = motor shaft angle (rad)

The motor torque, t, is linearly proportional the current through the armature. This is expressed as

As the armature rotates, a voltage difference, proportional to the rotational velocity of the armature shaft, is created. This voltage is called the back emf voltage, where emf stands for electromotive force.

By using Newton's and Kirchoff's Laws, the following equations can be derived

By making use of the Laplace transform, the above two equations can be rewritten as

The last step is to combine these two equations, cancelling the I(s) term. This yields the transfer function for the DC motor.

Observe that the denominator of the transfer function is a second-order polynomial, which means there are two poles in the s-plane. Note that the numerator does not contain any s terms, therefore both zeros occur at s = infinity.

We can use MATLAB to plot the step response of the motor transfer function. First, we will choose approximate constant values for a hypothetical motor. In the MATLAB command window type (note, >> denotes the command prompt)

>> J = 0.01;
>> b = 0.1;
>> K = 0.01;
>> R = 1;
>> L = 0.5;

Now that the constants are defined, enter the numerator and denominator of the transfer function.

>> num = K;
>> den = [J*L J*R+L*b K^2+b*R];
>> G = tf(num,den);

The step response of the motor can now be simulated by the command

>> step(G);

MATLAB will produce the following plot

Notice from the plot that the system is overdamped, this can be verified by finding the roots of the denominator with the command

>> roots(den)

ans =

-9.9975
-2.0025

The roots are both unique and negative, which translates into a overdamped, stable transfer function.